This course is a natural sequel to:
- Modern Probability Theory, based on Lebesgue integration theory (tought here in ENS Lyon in L3S1)
- Markov chains and martingales in discrete time (tought here in ENS Lyon in M1S1).
The purpose is to explore some continuous-time stochastic processes, without aiming to go into stochastic calculus or the general theory of Markov processes.
Chapter I:
We start with the example of the Poisson process, then we discuss quickly the technical settings of conditional distribution and the Markovian formalism, in particular the strong Markov property of the Feller processes.
Chapter II:
We introduce and study the continuous-time Markov chains. We discuss the relation between the Markov transition semigroup and the matrix of intensities, including the Kolmogorov forward and backward equations, and the possibility of explosion in finite time. We also discuss invariant measures and the long-term behavior.
Chapter III:
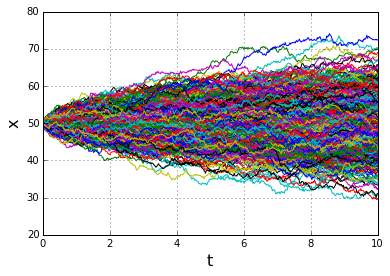
We introduce Brownian motion and discuss some of its properties.
Chapter IV:
We discuss quickly the martingales in continuous time and the stopping theorems.
Chapter V:
We discuss more subtle properties of Brownian motion and its relations to random walks, including Donsker invariance principle or Skorokhod embedding theorem.
Contenu du cours de géométrie avancée
- Variétés topologiques et différentiables. Définition et exemples de
variétés topologiques et différentiables. Unicité de structures
différentiables. Variétés différentiables à bord. Applications lisses.
Espace tangent. Différentielle d’une application. Submersions,
immersions, plongements.
Singularités d’une application lisse. Théorème du rang constant.
Points critiques, valeurs critiques, valeurs régulières. Sous-ensembles
négligeables d’une variété. Théorème de Sard. Partitions de l’unité.
Approximation des fonc- tions lisses par des immersions. Théorème
d’immersion et de plongement de Whitney (version facile). Transversalité.
Fibrés vectoriels. Rappels d’algèbre multilinéaire sur R :
applications multilinéaires, produit tensoriel, produit extérieur.
Définition de fibré vectoriel. Fibré tangent. Morphismes de fibrés
vectoriels. Opérations sur les fibrés vecto- riels. Trivialité des fibrés
vectoriels sur une base contractile.
Champs de vecteurs. Champs de tenseurs. Équations différentielles
autonomes sur une variété. Dérivée de Lie d’un champ de tenseurs. Crochet
de Lie de deux champs de vecteurs. Champs de vecteurs commutants.
Intégration sur variétés. Formes différentielles. Orientations et
formes volumes. Revêtement des orientations. Integration de formes
différentielles sur variétés orientées. Différentielle extérieure.
Théorème de Stokes.
Cohomologie et applications. Cohomologie de De Rham. Invariance par
homotopie de la cohomologie de De Rham. Lemme de Poincaré. Théorème de
Mayer-Vietoris. Cohomologie des sphères. Théorème de l’invariance de la
dimension. Théorème du point fixe de Brouwer.
This course is an introduction to commutative algebra (rings and modules).

